听说看过这篇文章的人，99 % 都背得了“常见的与对数有关的不等式”！

听说“常见的与对数有关的不等式”这一页课件很难背？

假的！看完这篇文章，你就能背完那一页的不等式！

先来个列表看看吧：

1. $e^x\ge x+1\Leftrightarrow x\ge \ln (x+1)\Leftrightarrow x-1\ge \ln x$，$e^{1-x}\le \cfrac{1}{x}\ (x>0)$
2. $\cfrac{x}{1+x}<\ln (1+x)<x\ (x>0)\ \Leftrightarrow\ \cfrac{x-1}{x}<\ln x<x-1\ (x>1)$
3. $\cfrac{2x}{x+2}<\ln (x+1)<\cfrac{1}{2}\left(x+\cfrac{x}{x+1}\right)\ (x>0)$
4. $x-\cfrac{1}{2}x^2<\ln (1+x)<\sqrt{x}\ (x>0)$
5. $\forall a>0,b>0,a\neq b$，有 $\sqrt{ab}<\cfrac{a-b}{\ln a-\ln b}<\cfrac{a+b}{2}$
6. $2\cfrac{x-1}{x+1}<\ln x<\cfrac{1}{2}\left(x-\cfrac{1}{x}\right)\ (x>1)$

六组不等式，看上去很吓人！怎么才能记住呢？读下去就知道了。

提示：点击文中的图片可以查看全图。

指数

泰勒展开系列

泰勒（马克劳林）展开 $e^x=1+x+\cfrac{x^2}{2}+\cfrac{x^3}{6}+\cdots+\cfrac{x^n}{n!}+\cdots$ 的衍生不等式，可以描述“$e^x$ 在 $x\ge 0$ 时增长得很快”的特征。

高考最常用的是 $e^x\ge x+1$，当且仅当 $x=0$ 时等号成立。

那么如何描述“$e^x$ 在 $x<0$ 时缓慢趋于 $0$”的特征呢？“缓慢趋于 $0$”的意思就是倒数趋于正无穷，因此上一个式子取倒数就可以得到 $e^{-x}\le \cfrac{1}{x+1}\ (x>-1)$，将 $x=x'-1$ 代入得 $e^{1-x'}\le \cfrac{1}{x'}\ (x'>0)$。小于另一个缓慢趋于 $0$ 的函数，这就可以刻画这一特征。

切线系列

$e^x\ge x+1$ 是在 $0$ 处的切线不等式，有时还会用到在 $1$ 处的切线不等式 $e^x\ge ex$，通常在式中明确出现 $e$ 时使用。如果有十足的把握，也可以尝试在其他地方的切线。

次数系列

$e^x$ 可以升到任意次，这在取点时比较好用。

对一切 $x\ge 0$，我们有 $e^x>x$ 和 $e^x>x^2$，但是三次以上就不行了；事实上，$e^x\ge x^e$，可以通过取对数进行证明。

当然，对任意大的 $n$，总存在充分大的 $x_0$，使得 $x> x_0$ 时 $e^x>x^n$。证明这一点有一个简单的方法，就是先证 $e^x>\cfrac{x^{n+1}}{(n+1)!}\ (x\ge 0)$，然后取 $\cfrac{x^{n+1}}{(n+1)!}>x^n$ 的点即可。

对数

泰勒展开系列

$\ln (x+1)=x-\cfrac{x^2}{2}+\cfrac{x^3}{3}-\cdots+(-1)^{n+1}\cfrac{x^n}{n}+\cdots$

最常用的还是 $\ln (x+1)\le x$，当且仅当 $x=0$ 时等号成立；常见的变形是令 $x'=x+1$，则 $\ln x'\le x-1$。当然有时会用到 $\ln (x+1)>x-\cfrac{x^2}{2}\ (x>0)$；这个式子在 $-1<x<0$ 时不等号反向。

如果我们需要对数的下界怎么办呢？在 $\ln x\le x-1$ 中，令 $t=\cfrac{1}{x}$，那么就有 $-\ln t\le \cfrac{1}{t}-1$，也就是 $\ln t\ge 1-\cfrac{1}{t}$。同理有 $\ln (t+1)\ge \cfrac{t}{t+1}$。

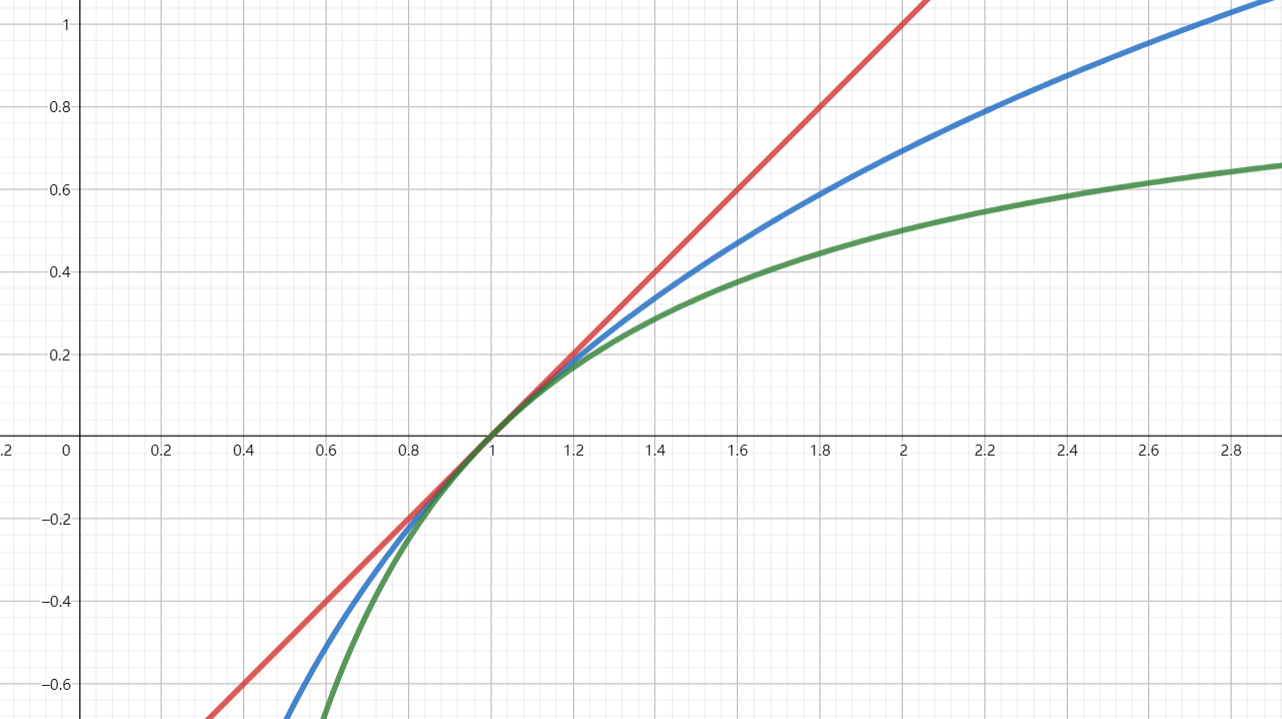
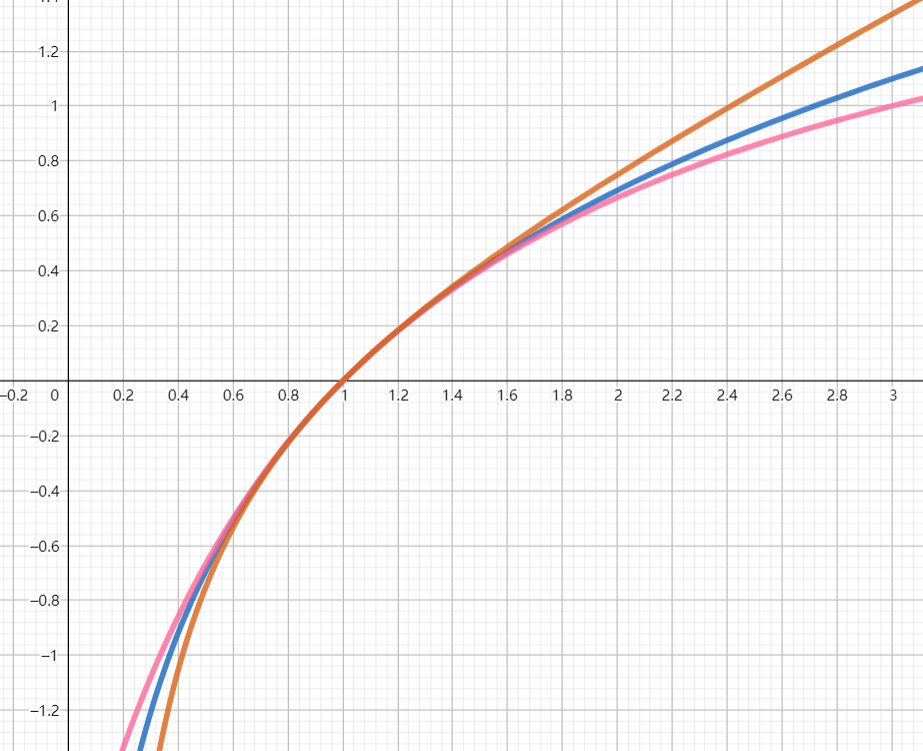
这样我们得到了一组 $\ln x$ 的上下界：$\cfrac{x-1}{x}\le \ln x\le x-1$，等号成立当且仅当 $x=1$。这组上下界的图如下：

顺带说一句，这个泰勒展开的收敛半径是 $1$，也就是至多只能用来暴力加和估算 $\ln 2$，但是求起来也很痛苦。下面附上一个巧妙地估算 $\ln 2$ 的过程。

$\ln 2=1-\frac{1}{2}+\frac{1}{3}-\frac{1}{4}+\cdots$

而 $\frac{1}{n}-\frac{1}{n+1}+\frac{1}{n+2}-\frac{1}{n+3}+\cdots=\frac{1}{n(n+1)}+\frac{1}{(n+2)(n+3)}+\cdots<\frac{1}{(n-0.5)(n+1.5)}+\frac{1}{(n+1.5)(n+3.5)}+\cdots=\frac{1}{2n-1}$（最后一个等号是裂项）

因此 $\ln 2<1-\frac{1}{2}+\frac{1}{3}-\frac{1}{4}+\frac{1}{5}-\frac{1}{6}+\frac{1}{7}-\frac{1}{8}+\frac{1}{17}<0.6934$

且有 $\ln 2>1-\frac{1}{2}+\frac{1}{3}-\frac{1}{4}+\frac{1}{5}-\frac{1}{11}>0.6924$

还可以用比较容易收敛的 $\ln \cfrac{1+x}{1-x}=2x+\cfrac{2x^3}{3}+\cfrac{2x^5}{5}+\cdots$ 来计算（把泰勒展开中的 $x$ 换为 $-x$，两式相加即得）。

次数系列

$\ln(x)$ 在渐进意义上小于 $x^a\ (a>0)$，但能使得 $\forall x>0,\ln (x+1)\le x^a$ 的 $a$ 的取值范围是什么呢？

这个问题好像很难解，分离参数会得到一个诡异的式子，画图可以得到 $a$ 的范围大概是 $0.3798312149<a\le 1$；不过有用的可能只有 $a=1$ 和 $a=\frac{1}{2}$，即 $\ln (x+1)< x$ 和 $\ln (x+1)<\sqrt{x}$。

对数平均不等式系列

我们都知道对数平均不等式，那与它对应的一组 $\ln x$ 的上下界是什么呢？

我们试图从头开始理解这一组上下界。下面，我们采用定积分的方法。

我们知道，$\int \frac{1}{x} \mathrm{d}x=\ln x+C$，因此或许可以用 $y=\frac{1}{x}$ 的图象下的面积对 $\ln x$ 进行放缩。

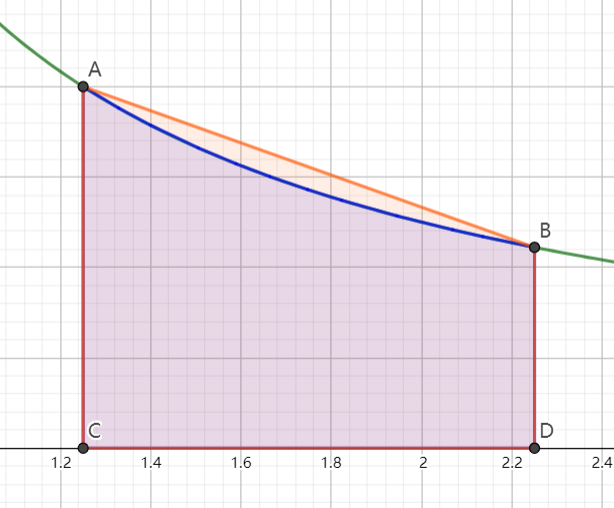
对 $x>0$，我们考虑 $\int ^{x+1}_{x} \frac{1}{x} \mathrm{d}x$。

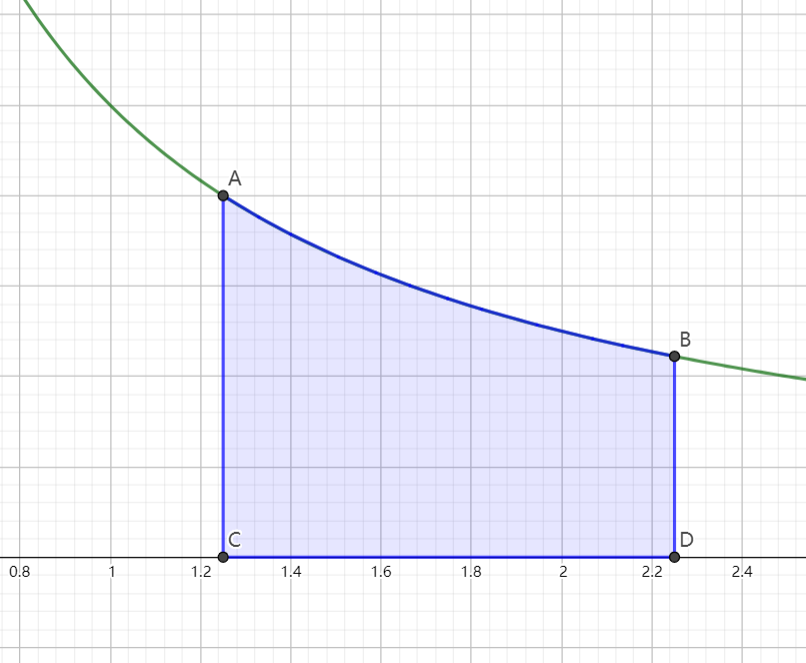
首先，这个值当然等于 $\ln \frac{x+1}{x}=\ln (1+\frac{1}{x})$，如图中的蓝色区域所示。

那么蓝色区域的面积显然小于下图中红色矩形的面积 $\cfrac{1}{x}$，且大于绿色矩形的面积 $\cfrac{1}{x+1}$（注意这两个矩形的宽都是 $1$）。

根据面积的大小关系，我们就可以得到 $\cfrac{1}{x+1} < \ln (1+\cfrac{1}{x})< \cfrac{1}{x}\ (x>0)$。令 $t=\cfrac{1}{x}$，我们就可以得到 $\cfrac{t}{t+1}< \ln (1+t)< t\ (t>0)$，即 $\cfrac{x-1}{x}< \ln x< x-1\ (x>1)$，也就是泰勒展开系列不等式的一部分！

如何得到另一部分（$0<x<1$）呢？令 $t=\cfrac{1}{x}$（这个 $t$ 和上一段的 $t$ 不一样，只是用了同一个符号而已），可以得到 $\cfrac{\cfrac{1}{t}-1}{\cfrac{1}{t}}< -\ln t< \cfrac{1}{t}-1\ (0<t<1)$，调整之后仍然是 $\cfrac{t-1}{t}<\ln t<t-1\ (0<t<1)$，即不等式方向没有改变。

再补上 $x=1$ 这一个点。$x=1$ 时这三个式子都是 $0$，所以取到等号。

综上，我们可以根据面积关系，并加以代数变形，证明$\cfrac{x-1}{x}\le \ln x\le x-1$，等号成立当且仅当 $x=1$。

这种方法能不能“生产”出别的不等式呢？

考虑这个问题：这两个矩形的面积和曲边梯形的面积差得比较大，能不能有更精确的呢？

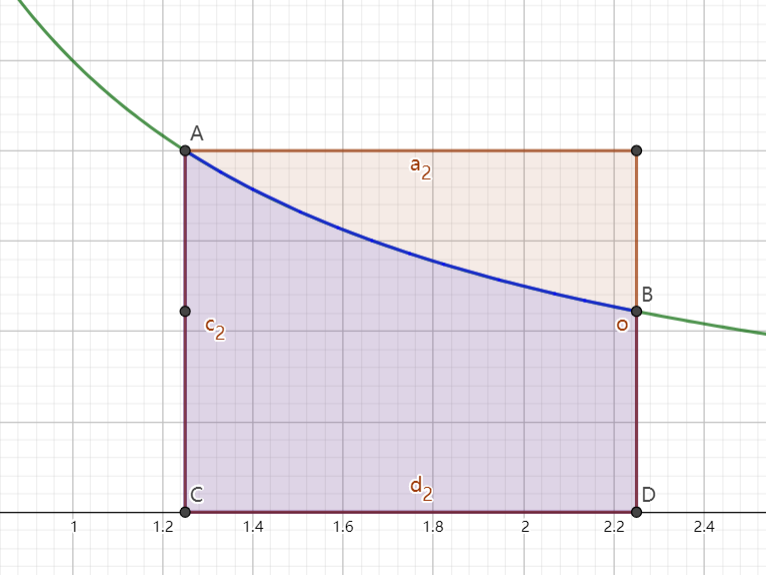
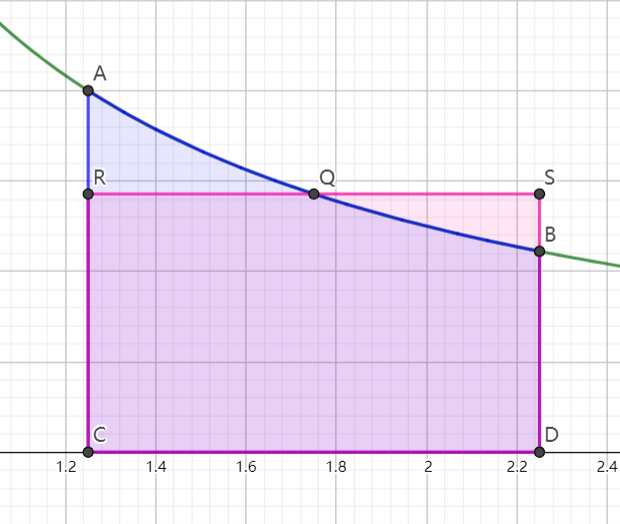
首先，我们可以考虑用梯形进行近似。如下图，蓝色区域的面积显然小于橙色梯形的面积 $\cfrac{1}{2}\left(\cfrac{1}{x}+\cfrac{1}{x+1}\right)$，这和 $y=\frac{1}{x}$ 是下凸函数有关。

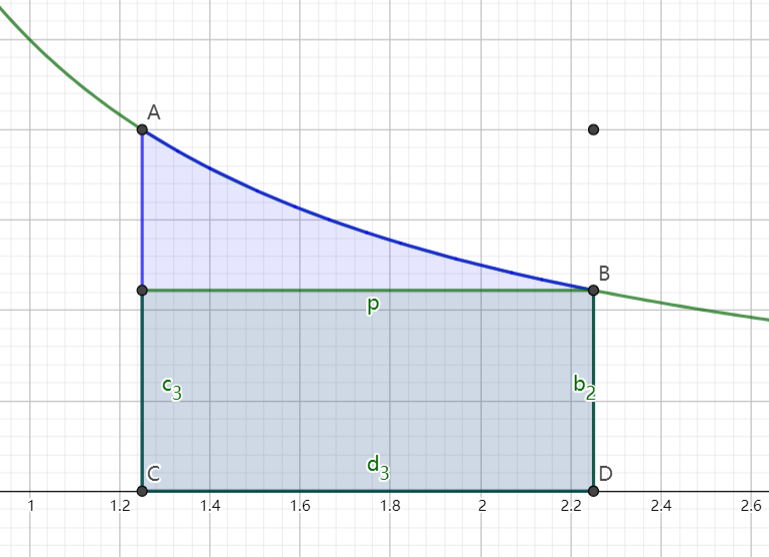
接着，我们还可以取中点进行矩形近似，也就是作以 $\cfrac{1}{\cfrac{x+(x+1)}{2}}$ 为高的矩形，如下图中的粉色矩形。这个矩形的面积就是 $\cfrac{2}{2x+1}$。

粉色区域和蓝色区域的面积大小关系如何呢？设 $m=x+\cfrac{1}{2}$，那么对于 $\Delta\in (0,\cfrac{1}{2}]$，有 $\cfrac{1}{m}-\cfrac{1}{m+\Delta}<\cfrac{1}{m-\Delta}-\cfrac{1}{m}$（同样是由于下凸），也就是与中点距离相同的情况下，右边的小块（$\mathrm{QBS}$）的“高度差”比左边小块（$\mathrm{QAR}$）的“高度差”小。用类似“祖暅原理”的思想，可以得到右边小块的面积小于左边小块的面积（看图也可以看出来），也就是蓝色区域的面积略大。

根据面积关系 $\text{粉色}<\text{蓝色}<\text{橙色}$，我们可以得到 $\cfrac{2}{2x+1}<\ln(1+\cfrac{1}{x})<\cfrac{1}{2}\left(\cfrac{1}{x}+\cfrac{1}{x+1}\right)\ (x>0)$。

像上面一样令 $t=\cfrac{1}{x}$，可以得到 $\cfrac{2t}{t+2}<\ln (1+t)<\cfrac{1}{2}(t+\cfrac{t}{1+t})\ (t>0)$；进一步令 $x=t+1$ 得到 $2\cfrac{x-1}{x+1}<\ln x<\cfrac{1}{2}\left(x-\cfrac{1}{x} \right)\ (x>1)$。

能不能补上 $0<x<1$ 时的情形呢？令 $t=\cfrac{1}{x}$（这个 $t$ 和上一段的 $t$ 也不一样），得到 $2\cfrac{t-1}{t+1}>\ln t>\cfrac{1}{2}\left(t-\cfrac{1}{t}\right)\ (0<t<1)$，不等号方向恰好反了过来。

$x=1$ 时三个式子都为 $0$，在这时取等号。

所以 $2\cfrac{x-1}{x+1}<\ln x<\cfrac{1}{2}\left(x-\cfrac{1}{x} \right)\ (x>1)$，$x=1$ 时取等号，$0<x<1$ 时不等号反向。这组上下界的图如下，特别注意粉色曲线、橙色曲线的相对位置改变（对应了不等号反向）。

还有一个对比图，可以看出这一组上下界比上一组上下界更紧。

大小顺序：$0<x<1,\ \text{绿}<\text{橙}<\textbf{蓝}<\text{粉}<\text{红}$；$x>1,\ \text{绿}<\text{粉}<\textbf{蓝}<\text{橙}<\text{红}$。

事实上，橙/粉 这一组上下界也可以直接通过代数推导（定积分）得到。

当 $x>1$ 时，由 $\forall t>1,\ 1-\cfrac{1}{t}<\ln t<t-1$ 知，$\int_{1}^{x}\left(1-\cfrac{1}{t}\right)\mathrm{d}t<\int_{1}^{x}\ln t\mathrm{d}t<\int_{1}^{x}(t-1)\mathrm{d}t$。

第一个式子，不定积分的结果是 $t-\ln t+C$，代入得到定积分的结果是 $x-1-\ln x$。

第三个式子，不定积分的结果是 $\cfrac{1}{2}t^2-t+C$，代入得到定积分的结果是 $\cfrac{1}{2}x^2-x+\cfrac{1}{2}$。

第二个式子的不定积分需要用到分部积分法，结果是 $t\ln t-t+C$（这个结果可以通过求导验证）。代入得到定积分的结果是 $x\ln x-x+1$。

代回不等式中，得到 $x-1-\ln x<x\ln x-x+1<\cfrac{1}{2}x^2-x+\cfrac{1}{2}\ (x>1)$。把这个式子拆成两个不等式分别进行化简，就可以得到 $2\cfrac{x-1}{x+1}<\ln x<\cfrac{1}{2}\left(x-\cfrac{1}{x} \right)\ (x>1)$ 了。

根据这个式子，就可以得出对数平均不等式了。

给定 $0<b<a$，我们来证明 $\sqrt{ab}<\cfrac{a-b}{\ln a-\ln b}<\cfrac{a+b}{2}$。

对 $\ln x>2\cfrac{x-1}{x+1}$，令 $x=\cfrac{a}{b}$，化简可以得到 $\cfrac{a-b}{\ln a-\ln b}<\cfrac{a+b}{2}$；对 $\ln x<\cfrac{1}{2}\left(x-\cfrac{1}{x}\right)$，令 $x=\sqrt{\cfrac{a}{b}}$，化简可以得到 $\sqrt{ab}<\cfrac{a-b}{\ln a-\ln b}$。连起来就可以得到对数平均不等式了。

能不能从对数平均不等式出发，得到 橙/粉 上下界呢？

在 $\cfrac{a-b}{\ln a-\ln b}<\cfrac{a+b}{2}$ 中，令 $a=x(x>1),b=1$，得到 $\ln x>2\cfrac{x-1}{x+1}$；在 $\sqrt{ab}<\cfrac{a-b}{\ln a-\ln b}$ 中，令 $a=x^2,b=1$，得到 $\ln x<\cfrac{1}{2}\left(x-\cfrac{1}{x}\right)$。在这个推导过程中，如果比较细心，可以发现，如果 $0<x<1$，会出现一次不等号反转。

看来对数平均不等式和这组上下界可以互推，也就是说，它们是等价的。于是我们可以把这组上下界叫做“对数平均不等式系列”。

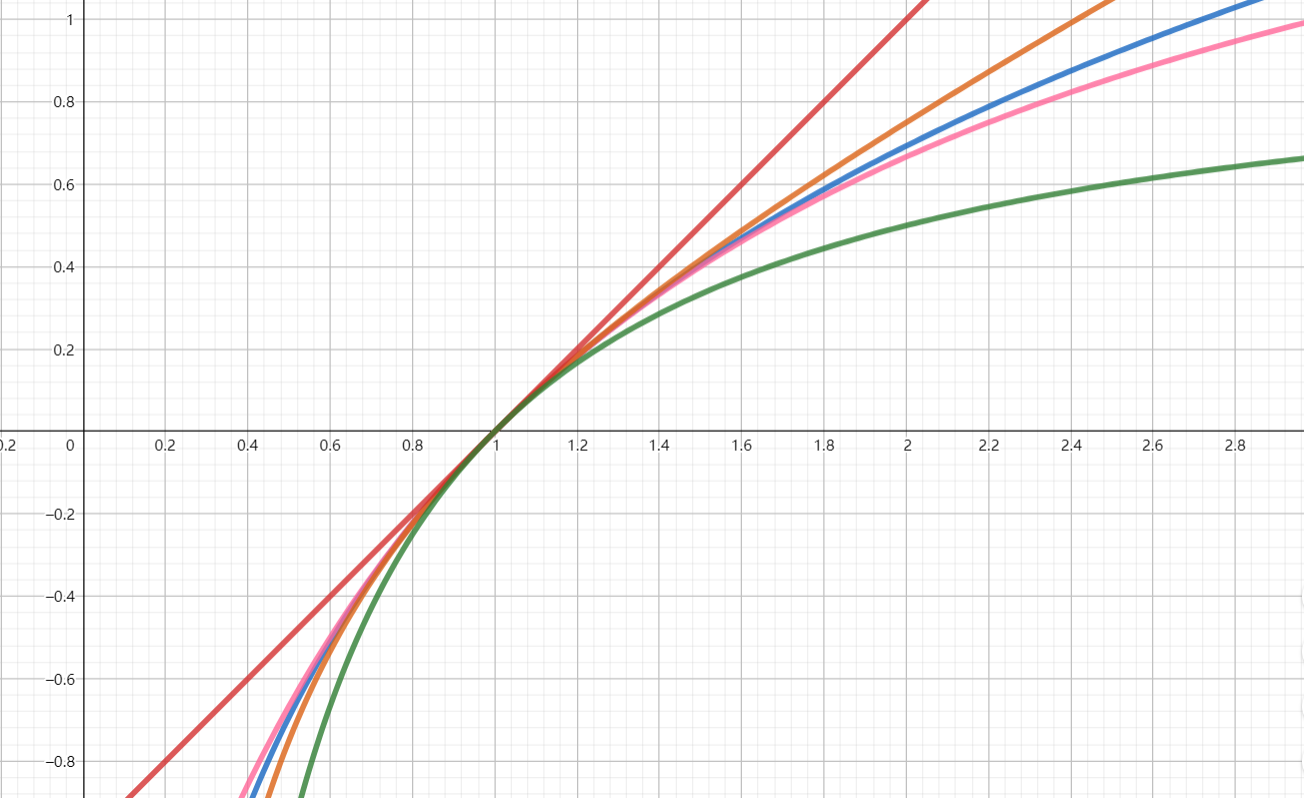
既然这组上下界和一个特定的不等式相联系，那么 $\cfrac{x-1}{x}<\ln x<x-1\ (x>1)$ 是否也和一个不等式有联系呢？我们把 $\ln x$ 写成 $\ln x-\ln 1$，三个式子同时除以 $x-1$ 得到 $\cfrac{1}{x}<\cfrac{\ln x-\ln 1}{x-1}<1$。由于 $\cfrac{1}{x}$ 是 $\ln x$ 的导数，因此令 $f(x)=\ln x$，这个式子就可以写成 $f'(x)<\cfrac{f(x)-f(1)}{x-1}<f'(1)$，再结合 $f'(x)$ 单调减，这不就是拉格朗日中值定理吗？当然，中值定理和泰勒展开还是有很大的联系的（还记得那个 费马引理 - 泰勒展开 - 拉格朗日中值定理 - 洛必达法则 的图么）。

说了这么多废话，都是希望能借助不等式的背景，更好地记住这些不等式，同时能够更灵活地运用。

泰勒展开与不等式

我们不难得出一些简单函数的泰勒展开，那么能不能借助泰勒展开得到不等式进行放缩呢？

首先考虑一种平凡的情形。如果 $\forall x\ge x_0,f(x)\ge f(x_0)$，那么可以得到 $\forall x\ge x_0,f(x)\ge f(x_0)$。这不是废话嘛，条件和结论完全一样——啊，这就是“平凡”这个词的意思了，放心，后面的会有用的。

接着考虑一种简单的情形。如果 $\forall x\ge x_0,f'(x)\ge f'(x_0)$，那么是否可以得到 $\forall x\ge x_0,f(x)\ge f'(x_0)(x-x_0)+f(x_0)$，也就是函数图象在切线的上方呢？答案是肯定的，令 $g(x)=f(x)-f'(x_0)(x-x_0)-f(x_0)$，那么 $g(x_0)=0$。$g'(x)=f'(x)-f'(x_0)\ge 0$，得到 $g(x)$ 增，于是命题得证。

再考虑一种稍复杂的情形。如果 $\forall x\ge x_0,f''(x)\ge f''(x_0)$，那么是否可以得到 $\forall x\ge x_0,f(x)\ge \cfrac{1}{2}f''(x_0)(x-x_0)^2+f'(x_0)(x-x_0)+f(x_0)$ 呢？答案也是肯定的。令 $h(x)=f(x)-\cfrac{1}{2}f''(x_0)(x-x_0)^2-f'(x_0)(x-x_0)-f(x_0)$，那么 $h(x_0)=0$。$h'(x)=f'(x)-f''(x_0)(x-x_0)-f'(x_0)$。这里再求导就可以得到答案（这也是考试中的写法），但是我们可以取个巧！在上一段的结论中，令 $f_{\text{上一段}}(x)=f_{这一段}'(x)$，就是把 $f'(x)$ 当做主函数代入到上一段的结论中，就可以得到 $f'(x)\ge f''(x_0)(x-x_0)+f'(x_0)$，也就是 $h'(x)\ge 0$ 了！那么得到 $h(x)$ 增，命题又可以得证了。

当然，如果不理解“取巧”的方法，这里给出再求一次导的方法（本质是一样的）。$h'(x_0)=0$。$h''(x)=f''(x)-f''(x_0)\ge 0$，得到 $h'(x)$ 增，于是 $h'(x)\ge h'(x_0)=0$。

根据这三个式子，我们可以总结出：

如果 $\forall x\ge x_0, f^{(n)}(x)\ge f^{(n)}(x_0)$，那么就有 $\forall x\ge x_0,f(x)\ge T_n=f(x_0)+\cfrac{f'(x_0)}{1!}(x-x_0)+\cfrac{f''(x_0)}{2!}(x-x_0)^2+\cdots +\cfrac{f^{(n)}(x_0)}{n!}(x-x_0)^n$。

事实上，很多含参不等式恒成立问题都是这么改造来的（这就是我们很熟悉这个过程的原因）。我们也可以用这个方法构造出一些不等式用于放缩，但是很有可能不起作用；通常做题时还是以题目提示为主。

总结

先总结一下这六个系列的不等式。

• 指数的泰勒展开系列，主要是在 $x=0$ 处的展开 $e^x\ge x+1$；这个式子衍生出了很多带有 $e^x$ 的不等式；取倒数可以得到一个 $e^x$ 小于等于多少的式子。
• 指数的切线系列，可以尝试在任意地方的切线，典型的有 $e^x\ge ex$。
• 指数的次数系列，放到多少次都行。
• 对数的泰勒展开系列，最常用的还是 $\ln x\le x-1$，令 $t=\cfrac{1}{x}$ 可以得到 $\ln t$ 的下界。这组不等式还可以用拉格朗日中值定理（区间端点取 $1$ 和 $x$）记忆。注意，对数的不等式通常有 $\ln x$ 和 $\ln(x+1)$ 两种版本，只需要记一种，用到的时候换元就可以了。
• 对数的次数系列，常用的有 $\ln (1+x)\le x,\ \ln (1+x)<\sqrt{x}$。
• 对数平均不等式系列，包括对数平均不等式本身和一组上下界 $2\cfrac{x-1}{x+1}<\ln x<\cfrac{1}{2}\left(x-\cfrac{1}{x} \right)\ (x>1)$。对数平均不等式比较好记，如果记不清那一组上下界可以用对数平均不等式代入 $(x,1)$ 和 $(x^2,1)$ 得到。答题的时候则是用这组上下界构造函数来证明对数平均值不等式。

这六个系列的不等式是不是很好记？那么是时候兑现我们的诺言了，如何记住那六组不等式呢？

仔细观察可以发现，第一组不等式包括了指数泰勒展开系列和对数泰勒展开系列；第二组不等式是对数的泰勒展开系列；第三组、第五组和第六组说的都是对数平均不等式系列；第四组不等式说的是对数的次数系列。你看，这不就记住了吗？

所以，数学学习可以不死记硬背，而是通过加强理解和了解背景，更好地掌握知识。

参考资料

如果想进一步加深理解，可以读一下这两篇文章。

【导数压轴题】所谓“放缩”——简单函数不等式

【导数压轴题】再谈“放缩”——几个进阶不等式